3.14 Analysis of a Table of Distances
The following formula gives the distance between two individuals \(i\) and \(\ell\)
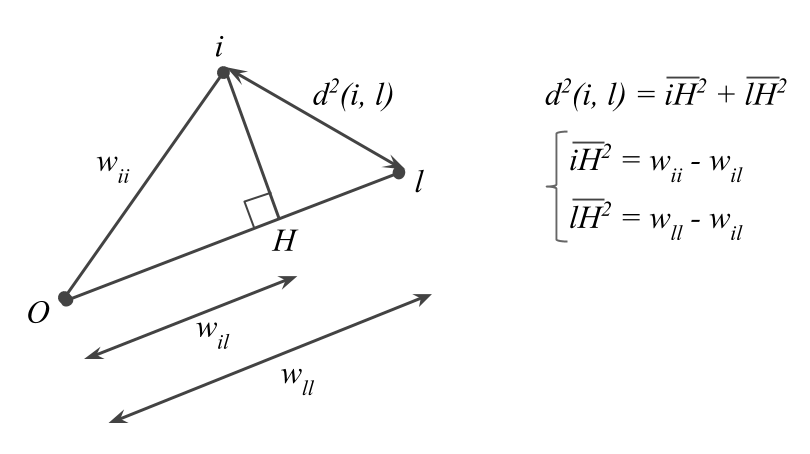
\[ d^2(i, \ell) = w_{ii} + w_{i\ell} - 2w_{i\ell} \tag{3.10} \]
where:
\(w_{ii} = \sum_{j}^{p} x^2_{ij}\) is the squared distance of the \(i\)-th point to the origin,
\(w_{i\ell} = \sum_{j}^{p} x_{ij} x_{\ell j}\) is the inner product between points \(i\) and \(\ell\).
Some times the input data is not the matrix \(\mathbf{X}\) of original variables, but the symmetric table of distances between pairs of individuals.
From these distances, it is possible to obtain a representation of the points, in a low dimensional space, that reflects as much as possible the real distances between individuals (in the original space).
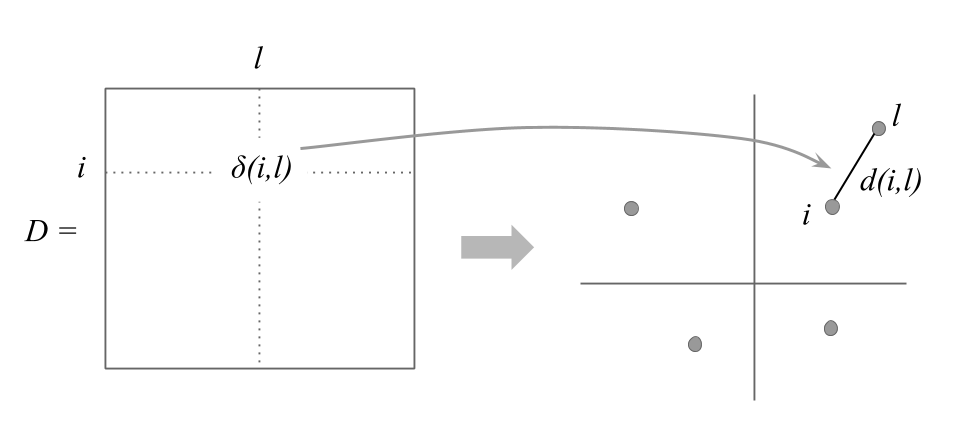
Figure 3.12: Distances in a low dimensional space
To carry out a PCA on the table of distances \(\mathbf{D}\), we must first convert this table into a matrix of inner products \(\mathbf{W}\), using the formula below:
\[ w_{i\ell} = \frac{1}{2} \big( d^2_{i\cdot} + d^2_{\ell \cdot} - d^2_{\cdot\cdot} - d^2(i, \ell) \big) \tag{3.11} \]
where:
\[ d^2_{i \cdot} = \frac{1}{n} \sum_{\ell} d^2(i, \ell) \quad \mathrm{and} \quad d^2_{\cdot \cdot} = \frac{1}{n^2} \sum_{i} \sum_{\ell} d^2(i, \ell) \]
Then, by diagonalizing matrix \(\mathbf{W}\), we obtain a set of eigenvalues and eigenvectors that provide an optimal solution to the problem.
The analysis of a table of distances via PCA is a completely generic technique. The reason for this is because PCA is applicable to any table of distances.
If the table of distances has the usual distances of a normalized PCA, then this analysis is identical to the one obtained on the cloud of individuals.
We should mention, though, that working with tables of distances, involves losing the relationship between the rows and columns. This loss prevents us from having access to the simultaneous representations of PCA when applied to a table \(\mathbf{X}\) of individuals and variables.
We should also say that, in order to place an illustrative individual on the low dimensional space, we need to know the distance of this individual to all the active points.