5.5 Projection of the cloud of points on a line

The projection of a point can be obtained by the scalar product of the point and the unit vector \(\mathbf{u}\) defining the line on which the projection is performed.

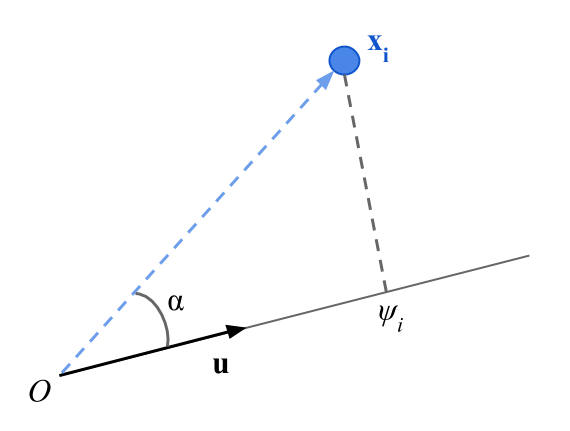
\[ \psi_i = \|\mathbf{x}\| \hspace{1mm} \|\mathbf{u}\| \hspace{1mm} cos(\alpha) = \sum_{j=1}^{p} x_{ij} u_j \]

with

\[ \|\mathbf{u}\|^2 = \sum_{j=1}^{p} u_{j}^{2} = 1 \]

The inertia of the projected cloud on a line is the variance of the projections on the line \(\mathbf{u}\). The square root of the variance is called standard deviation.

\[ I_u = \sum_{i=1}^{n} p_i \hspace{1mm} \psi_{i}^{2} \]

with

\[ \sum_{i=1}^{n} \psi_i = 0 \]

There is an equivalence between the mechanics notion of Inertia and the statistical notion of Variance.