5.1 Space of p-Dimensions

The objects that surround us are in a three dimensional space. Each object is defined by its coordinates in a basis formed by an origin and three orthogonal axes.

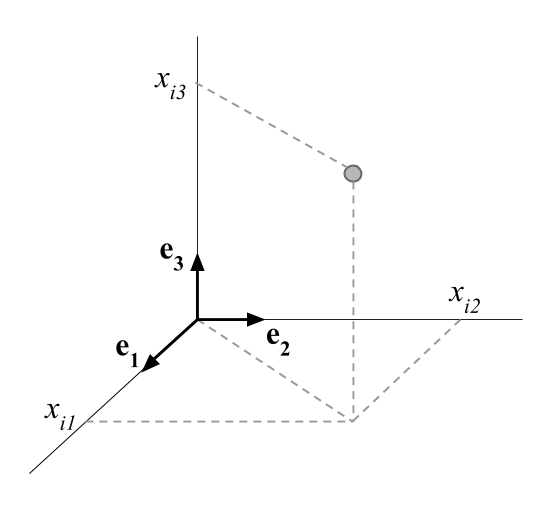
The axes are defined by vectors of unit length the provide a direction to each axis. The three vectors \((\mathbf{e_1}, \mathbf{e_2}, \mathbf{e_3})\) define a basis in the space of three dimensions. We can actually define various basis for the same space.

It is possible to generalize the space of three dimensions to spaces of higher dimensions. However, objects in spaces of dimensions greater than three cannot be visualized.

The points located in a space of \(p\) dimensions are defined by their \(p\) coordinates on the associated \(p\) axes:

\[ i \longrightarrow (x_{i1}, x_{i2}, \dots, x_{ip}) \]

This kind of multidmensional spaces are introduced in data analysis methods in order to map each point to a row of a data table. The coordinates are defined by the values of the row. Geometrically, these points are located in a space of as many dimensions as number of columns in the table.

Analogously, the columns of the table (i.e. the variables) can be regarded as points in a space in which the coordinates are the values of the column.