5.7 Correlation Coefficient

The correlation coefficient is a measure of the association between two variables when such association is linear.

We calculate the correlation coefficient by centering and normalizing the variables:

\[ cor(\mathbf{x_j}, \mathbf{x_k}) = \sum_{i=1}^{n} p_i \left ( \frac{x_{ij} - \bar{x}_j}{s_j} \right ) \left ( \frac{x_{ik} - \bar{x}_k}{s_k} \right ) \]

The correlation coefficient can be interpreted as the scalar product of two standardized variables. Given that the distance to the origin of these variables is equal to one, we see that the correlation between two variables coincides with the cosine of the angle formed by them.

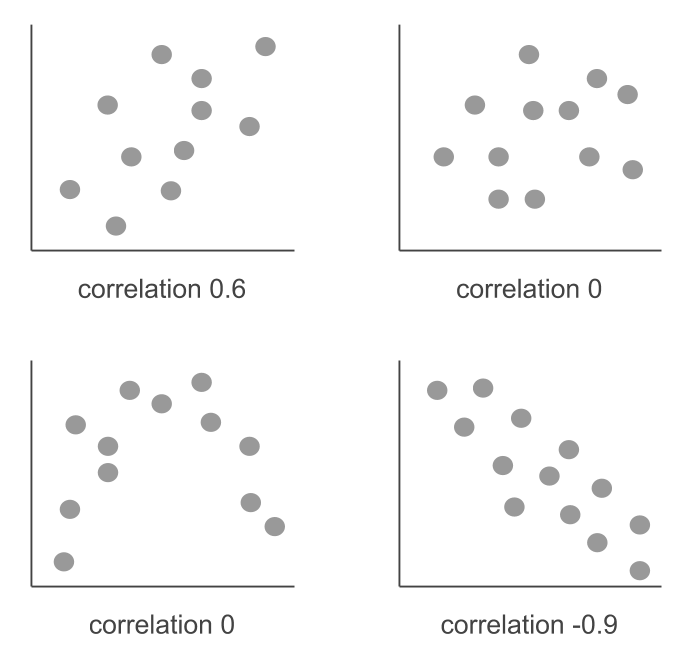
The correlation coefficient ranges between -1 and +1. When the correlation is equal to 1, this indicates that there is a perfect lineal association between the two variables. A correlation coefficient equal to -1 indicates that there is a perfect inverse lineal association. A correlation coefficient equals to zero may indicate an absence of association between the two variables, although it may also hide a non linear association (e.g. quadratic).

After having calculated a correlation coefficient of a sample, it can be interesting to ask whether this coefficient corresponds to a null correlation within the population. To answer this question, we can conduct a hypothesis test assuming that:

\[\begin{align*} E_{H_0} (r) &= 0 \\ & \\ var_{H_0} (r) &= \frac{1}{n-1} \end{align*}\]

When we are close to a value of 0, we have symmetry in the distribution of the coefficient of correlation. Therefore, under the null hypothesis we assume that the distribution of the correlation is approximately normal. We reject the null hypothesis, at the 5% significance level, if the correlation coefficient is larger than \(\pm 2 / \sqrt{n-1}\).